Các dạng bài tập toán hình học thi vào lớp 10 THPT
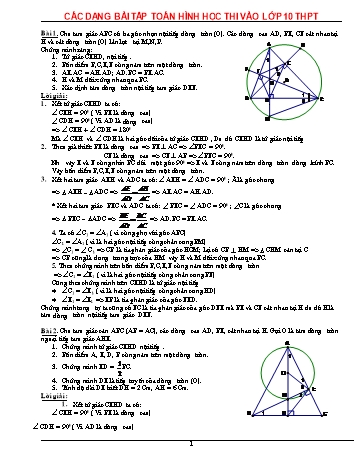
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại
H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng:
Tứ giác CEHD, nội tiếp .
Bốn điểm B,C,E,F cùng nằm trên một đường tròn.
AE.AC = AH.AD; AD.BC = BE.AC.
H và M đối xứng nhau qua BC.
Xác định tâm đường tròn nội tiếp tam giác DEF.
Lời giải:
Xét tứ giác CEHD ta có:
é CEH = 900 ( Vì BE là đường cao)
é CDH = 900 ( Vì AD là đường cao)
=> é CEH + é CDH = 1800
Mà é CEH và é CDH là hai góc đối của tứ giác CEHD , Do đó CEHD là tứ giác nội tiếp
Theo giả thiết: BE là đường cao => BE ^ AC => éBEC = 900.
CF là đường cao => CF ^AB => éBFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
Xét hai tam giác AEH và ADC ta có: é AEH = é ADC = 900 ; Â là góc chung
=> D AEH ~ DADC => => AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: é BEC = é ADC = 900 ; éC là góc chung
=> D BEC ~ DADC => => AD.BC = BE.AC.
4. Ta có éC1 = éA1 ( vì cùng phụ với góc ABC)
éC2 = éA1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> éC1 = é C2 => CB là tia phân giác của góc HCM; lại có CB ^ HM => D CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B,C,E,F cùng nằm trên một đường tròn
=> éC1 = éE1 ( vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
éC1 = éE2 ( vì là hai góc nội tiếp cùng chắn cung HD)
éE1 = éE2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.
Tóm tắt nội dung tài liệu: Các dạng bài tập toán hình học thi vào lớp 10 THPT
Bµi 1. Cho tam gi¸c ABC cã ba gãc nhän néi tiÕp ®êng trßn (O). C¸c ®êng cao AD, BE, CF c¾t nhau t¹i H vµ c¾t ®êng trßn (O) lÇn lît t¹i M,N,P. Chøng minh r»ng: Tø gi¸c CEHD, néi tiÕp . Bèn ®iÓm B,C,E,F cïng n»m trªn mét ®êng trßn. AE.AC = AH.AD; AD.BC = BE.AC. H vµ M ®èi xøng nhau qua BC. X¸c ®Þnh t©m ®êng trßn néi tiÕp tam gi¸c DEF. Lêi gi¶i: XÐt tø gi¸c CEHD ta cã: Ð CEH = 900 ( V× BE lµ ®êng cao) Ð CDH = 900 ( V× AD lµ ®êng cao) => Ð CEH + Ð CDH = 1800 Mµ Ð CEH vµ Ð CDH lµ hai gãc ®èi cña tø gi¸c CEHD , Do ®ã CEHD lµ tø gi¸c néi tiÕp Theo gi¶ thiÕt: BE lµ ®êng cao => BE ^ AC => ÐBEC = 900. CF lµ ®êng cao => CF ^ AB => ÐBFC = 900. Nh vËy E vµ F cïng nh×n BC díi mét gãc 900 => E vµ F cïng n»m trªn ®êng trßn ®êng kÝnh BC. VËy bèn ®iÓm B,C,E,F cïng n»m trªn mét ®êng trßn. XÐt hai tam gi¸c AEH vµ ADC ta cã: Ð AEH = Ð ADC = 900 ; ¢ lµ gãc chung => D AEH ~ DADC => => AE.AC = AH.AD. * XÐt hai tam gi¸c BEC vµ ADC ta cã: Ð BEC = Ð ADC = 900 ; ÐC lµ gãc chung => D BEC ~ DADC => => AD.BC = BE.AC. 4. Ta cã ÐC1 = ÐA1 ( v× cïng phô víi gãc ABC) ÐC2 = ÐA1 ( v× lµ hai gãc néi tiÕp cïng ch¾n cung BM) => ÐC1 = Ð C2 => CB lµ tia ph©n gi¸c cña gãc HCM; l¹i cã CB ^ HM => D CHM c©n t¹i C => CB còng lµ ®¬ng trung trùc cña HM vËy H vµ M ®èi xøng nhau qua BC. 5. Theo chøng minh trªn bèn ®iÓm B,C,E,F cïng n»m trªn mét ®êng trßn => ÐC1 = ÐE1 ( v× lµ hai gãc néi tiÕp cïng ch¾n cung BF) Còng theo chøng minh trªn CEHD lµ tø gi¸c néi tiÕp ÐC1 = ÐE2 ( v× lµ hai gãc néi tiÕp cïng ch¾n cung HD) ÐE1 = ÐE2 => EB lµ tia ph©n gi¸c cña gãc FED. Chøng minh t¬ng tù ta còng cã FC lµ tia ph©n gi¸c cña gãc DFE mµ BE vµ CF c¾t nhau t¹i H do ®ã H lµ t©m ®êng trßn néi tiÕp tam gi¸c DEF. Bµi 2. Cho tam gi¸c c©n ABC (AB = AC), c¸c ®êng cao AD, BE, c¾t nhau t¹i H. Gäi O lµ t©m ®êng trßn ngo¹i tiÕp tam gi¸c AHE. Chøng minh tø gi¸c CEHD néi tiÕp . Bèn ®iÓm A, E, D, B cïng n»m trªn mét ®êng trßn. Chøng minh ED = BC. Chøng minh DE lµ tiÕp tuyÕn cña ®êng trßn (O). TÝnh ®é dµi DE biÕt DH = 2 Cm, AH = 6 Cm. Lêi gi¶i: XÐt tø gi¸c CEHD ta cã: Ð CEH = 900 ( V× BE lµ ®êng cao) Ð CDH = 900 ( V× AD lµ ®êng cao) => Ð CEH + Ð CDH = 1800 Mµ Ð CEH vµ Ð CDH lµ hai gãc ®èi cña tø gi¸c CEHD , Do ®ã CEHD lµ tø gi¸c néi tiÕp 2. Theo gi¶ thiÕt: BE lµ ®êng cao => BE ^ AC => ÐBEA = 900. AD lµ ®êng cao => AD ^ BC => ÐBDA = 900. Nh vËy E vµ D cïng nh×n AB díi mét gãc 900 => E vµ D cïng n»m trªn ®êng trßn ®êng kÝnh AB. VËy bèn ®iÓm A, E, D, B cïng n»m trªn mét ®êng trßn. 3. Theo gi¶ thiÕt tam gi¸c ABC c©n t¹i A cã AD lµ ®êng cao nªn còng lµ ®êng trung tuyÕn => D lµ trung ®iÓm cña BC. Theo trªn ta cã ÐBEC = 900 . VËy tam gi¸c BEC vu«ng t¹i E cã ED lµ trung tuyÕn => DE = BC. V× O lµ t©m ®êng trßn ngo¹i tiÕp tam gi¸c AHE nªn O lµ trung ®iÓm cña AH => OA = OE => tam gi¸c AOE c©n t¹i O => ÐE1 = ÐA1 (1). Theo trªn DE = BC => tam gi¸c DBE c©n t¹i D => ÐE3 = ÐB1 (2) Mµ ÐB1 = ÐA1 ( v× cïng phô víi gãc ACB) => ÐE1 = ÐE3 => ÐE1 + ÐE2 = ÐE2 + ÐE3 Mµ ÐE1 + ÐE2 = ÐBEA = 900 => ÐE2 + ÐE3 = 900 = ÐOED => DE ^ OE t¹i E. VËy DE lµ tiÕp tuyÕn cña ®êng trßn (O) t¹i E. 5. Theo gi¶ thiÕt AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. ¸p dông ®Þnh lÝ Pitago cho tam gi¸c OED vu«ng t¹i E ta cã ED2 = OD2 – OE2 ó ED2 = 52 – 32 ó ED = 4cm Bµi 3 Cho nöa ®êng trßn ®êng kÝnh AB = 2R. Tõ A vµ B kÎ hai tiÕp tuyÕn Ax, By. Qua ®iÓm M thuéc nöa ®êng trßn kÎ tiÕp tuyÕn thø ba c¾t c¸c tiÕp tuyÕn Ax , By lÇn lît ë C vµ D. C¸c ®êng th¼ng AD vµ BC c¾t nhau t¹i N. Chøng minh AC + BD = CD. Chøng minh ÐCOD = 900. 3.Chøng minh AC. BD = . 4.Chøng minh OC // BM 5.Chøng minh AB lµ tiÕp tuyÕn cña ®êng trßn ®êng kÝnh CD. 5.Chøng minh MN ^ AB. 6.X¸c ®Þnh vÞ trÝ cña M ®Ó chu vi tø gi¸c ACDB ®¹t gi¸ trÞ nhá nhÊt. Lêi gi¶i: Theo tÝnh chÊt hai tiÕp tuyÕn c¾t nhau ta cã: CA = CM; DB = DM => AC + BD = CM + DM. Mµ CM + DM = CD => AC + BD = CD Theo tÝnh chÊt hai tiÕp tuyÕn c¾t nhau ta cã: OC lµ tia ph©n gi¸c cña gãc AOM; OD lµ tia ph©n gi¸c cña gãc BOM, mµ ÐAOM vµ ÐBOM lµ hai gãc kÒ bï => ÐCOD = 900. Theo trªn ÐCOD = 900 nªn tam gi¸c COD vu«ng t¹i O cã OM ^ CD ( OM lµ tiÕp tuyÕn ). ¸p dông hÖ thøc gi÷a c¹nh vµ ®êng cao trong tam gi¸c vu«ng ta cã OM2 = CM. DM, Mµ OM = R; CA = CM; DB = DM => AC. BD =R2 => AC. BD = . Theo trªn ÐCOD = 900 nªn OC ^ OD .(1) Theo tÝnh chÊt hai tiÕp tuyÕn c¾t nhau ta cã: DB = DM; l¹i cã OM = OB =R => OD lµ trung trùc cña BM => BM ^ OD .(2). Tõ (1) Vµ (2) => OC // BM ( V× cïng vu«ng gãc víi OD). Gäi I lµ trung ®iÓm cña CD ta cã I lµ t©m ®êng trßn ngo¹i tiÕp tam gi¸c COD ®êng kÝnh CD cã IO lµ b¸n kÝnh. Theo tÝnh chÊt tiÕp tuyÕn ta cã AC ^ AB; BD ^ AB => AC // BD => tø gi¸c ACDB lµ h×nh thang. L¹i cã I lµ trung ®iÓm cña CD; O lµ trung ®iÓm cña AB => IO lµ ®êng trung b×nh cña h×nh thang ACDB IO // AC , mµ AC ^ AB => IO ^ AB t¹i O => AB lµ tiÕp tuyÕn t¹i O cña ®êng trßn ®êng kÝnh CD 6. Theo trªn AC // BD => , mµ CA = CM; DB = DM nªn suy ra => MN // BD mµ BD ^ AB => MN ^ AB. 7. ( HD): Ta cã chu vi tø gi¸c ACDB = AB + AC + CD + BD mµ AC + BD = CD nªn suy ra chu vi tø gi¸c ACDB = AB + 2CD mµ AB kh«ng ®æi nªn chu vi tø gi¸c ACDB nhá nhÊt khi CD nhá nhÊt , mµ CD nhá nhÊt khi CD lµ kho¶ng c¸ch gi÷ Ax vµ By tøc lµ CD vu«ng gãc víi Ax vµ By. Khi ®ã CD // AB => M ph¶i lµ trung ®iÓm cña cung AB. Bµi 4 Cho tam gi¸c c©n ABC (AB = AC), I lµ t©m ®êng trßn néi tiÕp, K lµ t©m ®êng trßn bµng tiÕp gãc A , O lµ trung ®iÓm cña IK. Chøng minh B, C, I, K cïng n»m trªn mét ®êng trßn. Chøng minh AC lµ tiÕp tuyÕn cña ®êng trßn (O). TÝnh b¸n kÝnh ®êng trßn (O) BiÕt AB = AC = 20 Cm, BC = 24 Cm. Lêi gi¶i: (HD) 1. V× I lµ t©m ®êng trßn néi tiÕp, K lµ t©m ®êng trßn bµng tiÕp gãc A nªn BI vµ BK lµ hai tia ph©n gi¸c cña hai gãc kÒ bï ®Ønh B Do ®ã BI ^ BK hayÐIBK = 900 . T¬ng tù ta còng cã ÐICK = 900 nh vËy B vµ C cïng n»m trªn ®êng trßn ®êng kÝnh IK do ®ã B, C, I, K cïng n»m trªn mét ®êng trßn. Ta cã ÐC1 = ÐC2 (1) ( v× CI lµ ph©n gi¸c cña gãc ACH. ÐC2 + ÐI1 = 900 (2) ( v× ÐIHC = 900 ). ÐI1 = Ð ICO (3) ( v× tam gi¸c OIC c©n t¹i O) Tõ (1), (2) , (3) => ÐC1 + ÐICO = 900 hay AC ^ OC. VËy AC lµ tiÕp tuyÕn cña ®êng trßn (O). Tõ gi¶ thiÕt AB = AC = 20 Cm, BC = 24 Cm => CH = 12 cm. AH2 = AC2 – HC2 => AH = = 16 ( cm) CH2 = AH.OH => OH = = 9 (cm) OC = = 15 (cm) Bµi 5 Cho ®êng trßn (O; R), tõ mét ®iÓm A trªn (O) kÎ tiÕp tuyÕn d víi (O). Trªn ®êng th¼ng d lÊy ®iÓm M bÊt k× ( M kh¸c A) kÎ c¸t tuyÕn MNP vµ gäi K lµ trung ®iÓm cña NP, kÎ tiÕp tuyÕn MB (B lµ tiÕp ®iÓm). KÎ AC ^ MB, BD ^ MA, gäi H lµ giao ®iÓm cña AC vµ BD, I lµ giao ®iÓm cña OM vµ AB. Chøng minh tø gi¸c AMBO néi tiÕp. Chøng minh n¨m ®iÓm O, K, A, M, B cïng n»m trªn mét ®êng trßn . Chøng minh OI.OM = R2; OI. IM = IA2. Chøng minh OAHB lµ h×nh thoi. Chøng minh ba ®iÓm O, H, M th¼ng hµng. T×m quü tÝch cña ®iÓm H khi M di chuyÓn trªn ®êng th¼ng d Lêi gi¶i: (HS tù lµm). V× K lµ trung ®iÓm NP nªn OK ^ NP ( quan hÖ ®êng kÝnh Vµ d©y cung) => ÐOKM = 900. Theo tÝnh chÊt tiÕp tuyÕn ta cã ÐOAM = 900; ÐOBM = 900. nh vËy K, A, B cïng nh×n OM díi mét gãc 900 nªn cïng n»m trªn ®êng trßn ®êng kÝnh OM. VËy n¨m ®iÓm O, K, A, M, B cïng n»m trªn mét ®êng trßn. 3. Ta cã MA = MB ( t/c hai tiÕp tuyÕn c¾t nhau); OA = OB = R => OM lµ trung trùc cña AB => OM ^ AB t¹i I . Theo tÝnh chÊt tiÕp tuyÕn ta cã ÐOAM = 900 nªn tam gi¸c OAM vu«ng t¹i A cã AI lµ ®êng cao. ¸p dông hÖ thøc gi÷a c¹nh vµ ®êng cao => OI.OM = OA2 hay OI.OM = R2; vµ OI. IM = IA2. 4. Ta cã OB ^ MB (tÝnh chÊt tiÕp tuyÕn) ; AC ^ MB (gt) => OB // AC hay OB // AH. OA ^ MA (tÝnh chÊt tiÕp tuyÕn) ; BD ^ MA (gt) => OA // BD hay OA // BH. => Tø gi¸c OAHB lµ h×nh b×nh hµnh; l¹i cã OA = OB (=R) => OAHB lµ h×nh thoi. 5. Theo trªn OAHB lµ h×nh thoi. => OH ^ AB; còng theo trªn OM ^ AB => O, H, M th¼ng hµng( V× qua O chØ cã mét ®êng th¼ng vu«ng gãc víi AB). 6. (HD) Theo trªn OAHB lµ h×nh thoi. => AH = AO = R. VËy khi M di ®éng trªn d th× H còng di ®éng nhng lu«n c¸ch A cè ®Þnh mét kho¶ng b»ng R. Do ®ã quü tÝch cña ®iÓm H khi M di chuyÓn trªn ®êng th¼ng d lµ nöa ®êng trßn t©m A b¸n kÝnh AH = R Bµi 6 Cho tam gi¸c ABC vu«ng ë A, ®êng cao AH. VÏ ®êng trßn t©m A b¸n kÝnh AH. Gäi HD lµ ®êng kÝnh cña ®êng trßn (A; AH). TiÕp tuyÕn cña ®êng trßn t¹i D c¾t CA ë E. Chøng minh tam gi¸c BEC c©n. Gäi I lµ h×nh chiÕu cña A trªn BE, Chøng minh r»ng AI = AH. Chøng minh r»ng BE lµ tiÕp tuyÕn cña ®êng trßn (A; AH). Chøng minh BE = BH + DE. Lêi gi¶i: (HD) D AHC = DADE (g.c.g) => ED = HC (1) vµ AE = AC (2). V× AB ^CE (gt), do ®ã AB võa lµ ®êng cao võa lµ ®êng trung tuyÕn cña DBEC => BEC lµ tam gi¸c c©n. => ÐB1 = ÐB2 2. Hai tam gi¸c vu«ng ABI vµ ABH cã c¹nh huyÒn AB chung, ÐB1 = ÐB2 => D AHB = DAIB => AI = AH. 3. AI = AH vµ BE ^ AI t¹i I => BE lµ tiÕp tuyÕn cña (A; AH) t¹i I. 4. DE = IE vµ BI = BH => BE = BI+IE = BH + ED Bµi 7 Cho ®êng trßn (O; R) ®êng kÝnh AB. KÎ tiÕp tuyÕn Ax vµ lÊy trªn tiÕp tuyÕn ®ã mét ®iÓm P sao cho AP > R, tõ P kÎ tiÕp tuyÕn tiÕp xóc víi (O) t¹i M. Chøng minh r»ng tø gi¸c APMO néi tiÕp ®îc mét ®êng trßn. 2. Chøng minh BM // OP. 3. §êng th¼ng vu«ng gãc víi AB ë O c¾t tia BM t¹i N. Chøng minh tø gi¸c OBNP lµ h×nh b×nh hµnh. 4. BiÕt AN c¾t OP t¹i K, PM c¾t ON t¹i I; PN vµ OM kÐo dµi c¾t nhau t¹i J. Chøng minh I, J, K th¼ng hµng. Lêi gi¶i: (HS tù lµm). 2.Ta cã Ð ABM néi tiÕp ch¾n cung AM; Ð AOM lµ gãc ë t©m ch¾n cung AM => Ð ABM = (1) OP lµ tia ph©n gi¸c Ð AOM ( t/c hai tiÕp tuyÕn c¾t nhau ) => Ð AOP = (2) Tõ (1) vµ (2) => Ð ABM = Ð AOP (3) Mµ Ð ABM vµ Ð AOP lµ hai gãc ®ång vÞ nªn suy ra BM // OP. (4) 3.XÐt hai tam gi¸c AOP vµ OBN ta cã : ÐPAO=900 (v× PA lµ tiÕp tuyÕn ); ÐNOB = 900 (gt NO^AB). => ÐPAO = ÐNOB = 900; OA = OB = R; ÐAOP = ÐOBN (theo (3)) => DAOP = DOBN => OP = BN (5) Tõ (4) vµ (5) => OBNP lµ h×nh b×nh hµnh ( v× cã hai c¹nh ®èi song song vµ b»ng nhau). 4. Tø gi¸c OBNP lµ h×nh b×nh hµnh => PN // OB hay PJ // AB, mµ ON ^ AB => ON ^ PJ Ta còng cã PM ^ OJ ( PM lµ tiÕp tuyÕn ), mµ ON vµ PM c¾t nhau t¹i I nªn I lµ trùc t©m tam gi¸c POJ. (6) DÔ thÊy tø gi¸c AONP lµ h×nh ch÷ nhËt v× cã ÐPAO = ÐAON = ÐONP = 900 => K lµ trung ®iÓm cña PO ( t/c ®êng chÐo h×nh ch÷ nhËt). (6) AONP lµ h×nh ch÷ nhËt => ÐAPO = Ð NOP ( so le) (7) Theo t/c hai tiÕp tuyÕn c¾t nhau Ta cã PO lµ tia ph©n gi¸c ÐAPM => ÐAPO = ÐMPO (8). Tõ (7) vµ (8) => DIPO c©n t¹i I cã IK lµ trung tuyÕn ®«ng thêi lµ ®êng cao => IK ^ PO. (9) Tõ (6) vµ (9) => I, J, K th¼ng hµng. Bµi 8 Cho nöa ®êng trßn t©m O ®êng kÝnh AB vµ ®iÓm M bÊt k× trªn nöa ®êng trßn ( M kh¸c A,B). Trªn nöa mÆt ph¼ng bê AB chøa nöa ®êng trßn kÎ tiÕp tuyÕn Ax. Tia BM c¾t Ax t¹i I; tia ph©n gi¸c cña gãc IAM c¾t nöa ®êng trßn t¹i E; c¾t tia BM t¹i F tia BE c¾t Ax t¹i H, c¾t AM t¹i K. 1) Chøng minh r»ng: EFMK lµ tø gi¸c néi tiÕp. 2) Chøng minh r»ng: AI2 = IM . IB. 3) Chøng minh BAF lµ tam gi¸c c©n. 4) Chøng minh r»ng : Tø gi¸c AKFH lµ h×nh thoi. 5) X¸c ®Þnh vÞ trÝ M ®Ó tø gi¸c AKFI néi tiÕp ®îc mét ®êng trßn. Lêi gi¶i: 1. Ta cã : ÐAMB = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => ÐKMF = 900 (v× lµ hai gãc kÒ bï). ÐAEB = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => ÐKEF = 900 (v× lµ hai gãc kÒ bï). => ÐKMF + ÐKEF = 1800 . Mµ ÐKMF vµ ÐKEF lµ hai gãc ®èi cña tø gi¸c EFMK do ®ã EFMK lµ tø gi¸c néi tiÕp. Ta cã ÐIAB = 900 ( v× AI lµ tiÕp tuyÕn ) => DAIB vu«ng t¹i A cã AM ^ IB ( theo trªn). ¸p dông hÖ thøc gi÷a c¹nh vµ ®êng cao => AI2 = IM . IB. Theo gi¶ thiÕt AE lµ tia ph©n gi¸c gãc IAM => ÐIAE = ÐMAE => AE = ME (lÝ do ) => ÐABE =ÐMBE ( hai gãc néi tiÕp ch¾n hai cung b»ng nhau) => BE lµ tia ph©n gi¸c gãc ABF. (1) Theo trªn ta cã ÐAEB = 900 => BE ^ AF hay BE lµ ®êng cao cña tam gi¸c ABF (2). Tõ (1) vµ (2) => BAF lµ tam gi¸c c©n. t¹i B . BAF lµ tam gi¸c c©n. t¹i B cã BE lµ ®êng cao nªn ®ång thêi lµ ®¬ng trung tuyÕn => E lµ trung ®iÓm cña AF. (3) Tõ BE ^ AF => AF ^ HK (4), theo trªn AE lµ tia ph©n gi¸c gãc IAM hay AE lµ tia ph©n gi¸c ÐHAK (5) Tõ (4) vµ (5) => HAK lµ tam gi¸c c©n. t¹i A cã AE lµ ®êng cao nªn ®ång thêi lµ ®¬ng trung tuyÕn => E lµ trung ®iÓm cña HK. (6). Tõ (3) , (4) vµ (6) => AKFH lµ h×nh thoi ( v× cã hai ®êng chÐo vu«ng gãc víi nhau t¹i trung ®iÓm cña mçi ®êng). (HD). Theo trªn AKFH lµ h×nh thoi => HA // FK hay IA // FK => tø gi¸c AKFI lµ h×nh thang. §Ó tø gi¸c AKFI néi tiÕp ®îc mét ®êng trßn th× AKFI ph¶i lµ h×nh thang c©n. AKFI lµ h×nh thang c©n khi M lµ trung ®iÓm cña cung AB. ThËt vËy: M lµ trung ®iÓm cña cung AB => ÐABM = ÐMAI = 450 (t/c gãc néi tiÕp ). (7) Tam gi¸c ABI vu«ng t¹i A cã ÐABI = 450 => ÐAIB = 450 .(8) Tõ (7) vµ (8) => ÐIAK = ÐAIF = 450 => AKFI lµ h×nh thang c©n (h×nh thang cã hai gãc ®¸y b»ng nhau). VËy khi M lµ trung ®iÓm cña cung AB th× tø gi¸c AKFI néi tiÕp ®îc mét ®êng trßn. Bµi 9 Cho nöa ®êng trßn (O; R) ®êng kÝnh AB. KÎ tiÕp tuyÕn Bx vµ lÊy hai ®iÓm C vµ D thuéc nöa ®êng trßn. C¸c tia AC vµ AD c¾t Bx lÇn lît ë E, F (F ë gi÷a B vµ E). Chøng minh AC. AE kh«ng ®æi. Chøng minh Ð ABD = Ð DFB. Chøng minh r»ng CEFD lµ tø gi¸c néi tiÕp. Lêi gi¶i: C thuéc nöa ®êng trßn nªn ÐACB = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => BC ^ AE. ÐABE = 900 ( Bx lµ tiÕp tuyÕn ) => tam gi¸c ABE vu«ng t¹i B cã BC lµ ®êng cao => AC. AE = AB2 (hÖ thøc gi÷a c¹nh vµ ®êng cao ), mµ AB lµ ®êng kÝnh nªn AB = 2R kh«ng ®æi do ®ã AC. AE kh«ng ®æi. D ADB cã ÐADB = 900 ( néi tiÕp ch¾n nöa ®êng trßn ). => ÐABD + ÐBAD = 900 (v× tæng ba gãc cña mét tam gi¸c b»ng 1800)(1) D ABF cã ÐABF = 900 ( BF lµ tiÕp tuyÕn ). => ÐAFB + ÐBAF = 900 (v× tæng ba gãc cña mét tam gi¸c b»ng 1800) (2) Tõ (1) vµ (2) => ÐABD = ÐDFB ( cïng phô víi ÐBAD) Tø gi¸c ACDB néi tiÕp (O) => ÐABD + ÐACD = 1800 . ÐECD + ÐACD = 1800 ( V× lµ hai gãc kÒ bï) => ÐECD = ÐABD ( cïng bï víi ÐACD). Theo trªn ÐABD = ÐDFB => ÐECD = ÐDFB. Mµ ÐEFD + ÐDFB = 1800 ( V× lµ hai gãc kÒ bï) nªn suy ra ÐECD + ÐEFD = 1800, mÆt kh¸c ÐECD vµ ÐEFD lµ hai gãc ®èi cña tø gi¸c CDFE do ®ã tø gi¸c CEFD lµ tø gi¸c néi tiÕp. Bµi 10 Cho ®êng trßn t©m O ®êng kÝnh AB vµ ®iÓm M bÊt k× trªn nöa ®êng trßn sao cho AM < MB. Gäi M’ lµ ®iÓm ®èi xøng cña M qua AB vµ S lµ giao ®iÓm cña hai tia BM, M’A. Gäi P lµ ch©n ®êng vu«ng gãc tõ S ®Õn AB. 1.Gäi S’ lµ giao ®iÓm cña MA vµ SP. Chøng minh r»ng ∆ PS’M c©n. 2.Chøng minh PM lµ tiÕp tuyÕn cña ®êng trßn . Lêi gi¶i: 1. Ta cã SP ^ AB (gt) => ÐSPA = 900 ; ÐAMB = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => ÐAMS = 900 . Nh vËy P vµ M cïng nh×n AS díi mét gãc b»ng 900 nªn cïng n»m trªn ®êng trßn ®êng kÝnh AS. VËy bèn ®iÓm A, M, S, P cïng n»m trªn mét ®êng trßn. 2. V× M’®èi xøng M qua AB mµ M n»m trªn ®êng trßn nªn M’ còng n»m trªn ®êng trßn => hai cung AM vµ AM’ cã sè ®o b»ng nhau => ÐAMM’ = ÐAM’M ( Hai gãc néi tiÕp ch¾n hai cung b»ng nhau) (1) Còng v× M’®èi xøng M qua AB nªn MM’ ^ AB t¹i H => MM’// SS’ ( cïng vu«ng gãc víi AB) => ÐAMM’ = ÐAS’S; ÐAM’M = ÐASS’ (v× so le trong) (2). => Tõ (1) vµ (2) => ÐAS’S = ÐASS’. Theo trªn bèn ®iÓm A, M, S, P cïng n»m trªn mét ®/ trßn => ÐASP=ÐAMP (néi tiÕp cïng ch¾n AP ) => ÐAS’P = ÐAMP => tam gi¸c PMS’ c©n t¹i P. 3. Tam gi¸c SPB vu«ng t¹i P; tam gi¸c SMS’ vu«ng t¹i M => ÐB1 = ÐS’1 (cïng phô víi ÐS). (3) Tam gi¸c PMS’ c©n t¹i P => ÐS’1 = ÐM1 (4) Tam gi¸c OBM c©n t¹i O ( v× cã OM = OB =R) => ÐB1 = ÐM3 (5). Tõ (3), (4) vµ (5) => ÐM1 = ÐM3 => ÐM1 + ÐM2 = ÐM3 + ÐM2 mµ ÐM3 + ÐM2 = ÐAMB = 900 nªn suy ra ÐM1 + ÐM2 = ÐPMO = 900 => PM ^ OM t¹i M => PM lµ tiÕp tuyÕn cña ®êng trßn t¹i M Bµi 11. Cho tam gi¸c ABC (AB = AC). C¹nh AB, BC, CA tiÕp xóc víi ®êng trßn (O) t¹i c¸c ®iÓm D, E, F . BF c¾t (O) t¹i I , DI c¾t BC t¹i M. Chøng minh : Tam gi¸c DEF cã ba gãc nhän. DF // BC. 3. Tø gi¸c BDFC néi tiÕp. 4. Lêi gi¶i: 1. (HD) Theo t/c hai tiÕp tuyÕn c¾t nhau ta cã AD = AF => tam gi¸c ADF c©n t¹i A => ÐADF = ÐAFD s® cung DF ÐDEF < 900 ( v× gãc DEF néi tiÕp ch¾n cung DE). Chøng minh t¬ng tù ta cã ÐDFE < 900; ÐEDF < 900. Nh vËy tam gi¸c DEF cã ba gãc nhän. 2. Ta cã AB = AC (gt); AD = AF (theo trªn) => => DF // BC. 3. DF // BC => BDFC lµ h×nh thang l¹i cã Ð B = ÐC (v× tam gi¸c ABC c©n) => BDFC lµ h×nh thang c©n do ®ã BDFC néi tiÕp ®îc mét ®êng trßn . 4. XÐt hai tam gi¸c BDM vµ CBF Ta cã Ð DBM = ÐBCF ( hai gãc ®¸y cña tam gi¸c c©n). ÐBDM = ÐBFD (néi tiÕp cïng ch¾n cung DI); Ð CBF = ÐBFD (v× so le) => ÐBDM = ÐCBF . => DBDM ~DCBF => Bµi 12 Cho ®êng trßn (O) b¸n kÝnh R cã hai ®êng kÝnh AB vµ CD vu«ng gãc víi nhau. Trªn ®o¹n th¼ng AB lÊy ®iÓm M (M kh¸c O). CM c¾t (O) t¹i N. §êng th¼ng vu«ng gãc víi AB t¹i M c¾t tiÕp tuyÕn t¹i N cña ®êng trßn ë P. Chøng minh : Tø gi¸c OMNP néi tiÕp. Tø gi¸c CMPO lµ h×nh b×nh hµnh. CM. CN kh«ng phô thuéc vµo vÞ trÝ cña ®iÓm M. Khi M di chuyÓn trªn ®o¹n th¼ng AB th× P ch¹y trªn ®o¹n th¼ng cè ®Þnh nµo. Lêi gi¶i: 1. Ta cã ÐOMP = 900 ( v× PM ^ AB ); ÐONP = 900 (v× NP lµ tiÕp tuyÕn ). Nh vËy M vµ N cïng nh×n OP díi mét gãc b»ng 900 => M vµ N cïng n»m trªn ®êng trßn ®êng kÝnh OP => Tø gi¸c OMNP néi tiÕp. 2. Tø gi¸c OMNP néi tiÕp => ÐOPM = Ð ONM (néi tiÕp ch¾n cung OM) Tam gi¸c ONC c©n t¹i O v× cã ON = OC = R => ÐONC = ÐOCN => ÐOPM = ÐOCM. XÐt hai tam gi¸c OMC vµ MOP ta cã ÐMOC = ÐOMP = 900; ÐOPM = ÐOCM => ÐCMO = ÐPOM l¹i cã MO lµ c¹nh chung => DOMC = DMOP => OC = MP. (1) Theo gi¶ thiÕt Ta cã CD ^ AB; PM ^ AB => CO//PM (2). Tõ (1) vµ (2) => Tø gi¸c CMPO lµ h×nh b×nh hµnh. 3. XÐt hai tam gi¸c OMC vµ NDC ta cã ÐMOC = 900 ( gt CD ^ AB); ÐDNC = 900 (néi tiÕp ch¾n nöa ®êng trßn ) => ÐMOC =ÐDNC = 900 l¹i cã ÐC lµ gãc chung => DOMC ~DNDC => => CM. CN = CO.CD mµ CO = R; CD = 2R nªn CO.CD = 2R2 kh«ng ®æi => CM.CN =2R2 kh«ng ®æi hay tÝch CM. CN kh«ng phô thuéc vµo vÞ trÝ cña ®iÓm M. 4. ( HD) DÔ thÊy DOMC = DDPO (c.g.c) => ÐODP = 900 => P ch¹y trªn ®êng th¼ng cè ®Þnh vu«ng gãc víi CD t¹i D. V× M chØ ch¹y trªn ®o¹n th¼ng AB nªn P chØ ch¹y trªn do¹n th¼ng A’ B’ song song vµ b»ng AB. Bµi 13 Cho tam gi¸c ABC vu«ng ë A (AB > AC), ®êng cao AH. Trªn nöa mÆt ph¼ng bê BC chøa ®iÓn A , VÏ nöa ®êng trßn ®êng kÝnh BH c¾t AB t¹i E, Nöa ®êng trßn ®êng kÝnh HC c¾t AC t¹i F. Chøng minh AFHE lµ h×nh ch÷ nhËt. BEFC lµ tø gi¸c néi tiÕp. AE. AB = AF. AC. Chøng minh EF lµ tiÕp tuyÕn chung cña hai nöa ®êng trßn . Lêi gi¶i: 1. Ta cã : ÐBEH = 900 ( néi tiÕp ch¾n nöc ®êng trßn ) => ÐAEH = 900 (v× lµ hai gãc kÒ bï). (1) ÐCFH = 900 ( néi tiÕp ch¾n nöc ®êng trßn ) => ÐAFH = 900 (v× lµ hai gãc kÒ bï).(2) ÐEAF = 900 ( V× tam gi¸c ABC vu«ng t¹i A) (3) Tõ (1), (2), (3) => tø gi¸c AFHE lµ h×nh ch÷ nhËt ( v× cã ba gãc vu«ng). 2. Tø gi¸c AFHE lµ h×nh ch÷ nhËt nªn néi tiÕp ®îc mét ®êng trßn =>ÐF1=ÐH1 (néi tiÕp ch¾n cung AE) . Theo gi¶ thiÕt AH ^BC nªn AH lµ tiÕp tuyÕn chung cña hai nöa ®êng trßn (O1) vµ (O2) => ÐB1 = ÐH1 (hai gãc néi tiÕp cïng ch¾n cung HE) => ÐB1= ÐF1 => ÐEBC+ÐEFC = ÐAFE + ÐEFC mµ ÐAFE + ÐEFC = 1800 (v× lµ hai gãc kÒ bï) => ÐEBC+ÐEFC = 1800 mÆt kh¸c ÐEBC vµ ÐEFC lµ hai gãc ®èi cña tø gi¸c BEFC do ®ã BEFC lµ tø gi¸c néi tiÕp. 3. XÐt hai tam gi¸c AEF vµ ACB ta cã ÐA = 900 lµ gãc chung; ÐAFE = ÐABC ( theo Chøng minh trªn) => DAEF ~DACB => => AE. AB = AF. AC. * HD c¸ch 2: Tam gi¸c AHB vu«ng t¹i H cã HE ^ AB => AH2 = AE.AB (*) Tam gi¸c AHC vu«ng t¹i H cã HF ^ AC => AH2 = AF.AC (**) Tõ (*) vµ (**) => AE. AB = AF. AC 4. Tø gi¸c AFHE lµ h×nh ch÷ nhËt => IE = EH => DIEH c©n t¹i I => ÐE1 = ÐH1 . DO1EH c©n t¹i O1 (v× cã O1E vµO1H cïng lµ b¸n kÝnh) => ÐE2 = ÐH2. => ÐE1 + ÐE2 = ÐH1 + ÐH2 mµ ÐH1 + ÐH2 = ÐAHB = 900 => ÐE1 + ÐE2 = ÐO1EF = 900 => O1E ^EF . Chøng minh t¬ng tù ta còng cã O2F ^ EF. VËy EF lµ tiÕp tuyÕn chung cña hai nöa ®êng trßn . Bµi 14 Cho ®iÓm C thuéc ®o¹n th¼ng AB sao cho AC = 10 Cm, CB = 40 Cm. VÏ vÒ mét phÝa cña AB c¸c nöa ®êng trßn cã ®êng kÝnh theo thø tù lµ AB, AC, CB vµ cã t©m theo thø tù lµ O, I, K. §êng vu«ng gãc víi AB t¹i C c¾t nöa ®êng trßn (O) t¹i E. Gäi M. N theo thø tù lµ giao ®iÓm cña EA, EB víi c¸c nöa ®êng trßn (I), (K). 1.Chøng minh EC = MN. 2.Ch/minh MN lµ tiÕp tuyÕn chung cña c¸c nöa ®/trßn (I), (K). 3.TÝnh MN. 4.TÝnh diÖn tÝch h×nh ®îc giíi h¹n bëi ba nöa ®êng trßn Lêi gi¶i: 1. Ta cã: ÐBNC= 900( néi tiÕp ch¾n nöa ®êng trßn t©m K) => ÐENC = 900 (v× lµ hai gãc kÒ bï). (1) ÐAMC = 900 ( néi tiÕp ch¾n nöc ®êng trßn t©m I) => ÐEMC = 900 (v× lµ hai gãc kÒ bï).(2) ÐAEB = 900 (néi tiÕp ch¾n nöa ®êng trßn t©m O) hay ÐMEN = 900 (3) Tõ (1), (2), (3) => tø gi¸c CMEN lµ h×nh ch÷ nhËt => EC = MN (tÝnh chÊt ®êng chÐo h×nh ch÷ nhËt ) 2. Theo gi¶ thiÕt EC ^AB t¹i C nªn EC lµ tiÕp tuyÕn chung cña hai nöa ®êng trßn (I) vµ (K) => ÐB1 = ÐC1 (hai gãc néi tiÕp cïng ch¾n cung CN). Tø gi¸c CMEN lµ h×nh ch÷ nhËt nªn => ÐC1= ÐN3 => ÐB1 = ÐN3.(4) L¹i cã KB = KN (cïng lµ b¸n kÝnh) => tam gi¸c KBN c©n t¹i K => ÐB1 = ÐN1 (5) Tõ (4) vµ (5) => ÐN1 = ÐN3 mµ ÐN1 + ÐN2 = ÐCNB = 900 => ÐN3 + ÐN2 = ÐMNK = 900 hay MN ^ KN t¹i N => MN lµ tiÕp tuyÕn cña (K) t¹i N. Chøng minh t¬ng tù ta còng cã MN lµ tiÕp tuyÕn cña (I) t¹i M, VËy MN lµ tiÕp tuyÕn chung cña c¸c nöa ®êng trßn (I), (K). 3. Ta cã ÐAEB = 900 (néi tiÕp ch¾n nöc ®êng trßn t©m O) => DAEB vu«ng t¹i A cã EC ^ AB (gt) => EC2 = AC. BC ó EC2 = 10.40 = 400 => EC = 20 cm. Theo trªn EC = MN => MN = 20 cm. 4. Theo gi¶ thiÕt AC = 10 Cm, CB = 40 Cm => AB = 50cm => OA = 25 cm Ta cã S(o) = .OA2 = 252 = 625; S(I) = . IA2 = .52 = 25; S(k) = .KB2 = . 202 = 400. Ta cã diÖn tÝch phÇn h×nh ®îc giíi h¹n bëi ba nöa ®êng trßn lµ S = ( S(o) - S(I) - S(k)) S = ( 625- 25- 400) = .200 = 100 314 (cm2) Bµi 15 Cho tam gi¸c ABC vu«ng ë A. Trªn c¹nh AC lÊy ®iÓm M, dùng ®êng trßn (O) cã ®êng kÝnh MC. ®êng th¼ng BM c¾t ®êng trßn (O) t¹i D. ®êng th¼ng AD c¾t ®êng trßn (O) t¹i S. Chøng minh ABCD lµ tø gi¸c néi tiÕp . Chøng minh CA lµ tia ph©n gi¸c cña gãc SCB. Gäi E lµ giao ®iÓm cña BC víi ®êng trßn (O). Chøng minh r»ng c¸c ®êng th¼ng BA, EM, CD ®ång quy. Chøng minh DM lµ tia ph©n gi¸c cña gãc ADE. Chøng minh ®iÓm M lµ t©m ®êng trßn néi tiÕp tam gi¸c ADE. Lêi gi¶i: Ta cã ÐCAB = 900 ( v× tam gi¸c ABC vu«ng t¹i A); ÐMDC = 900 ( gãc néi tiÕp ch¾n nöa ®êng trßn ) => ÐCDB = 900 nh vËy D vµ A cïng nh×n BC díi mét gãc b»ng 900 nªn A vµ D cïng n»m trªn ®êng trßn ®êng kÝnh BC => ABCD lµ tø gi¸c néi tiÕp. ABCD lµ tø gi¸c néi tiÕp => ÐD1= ÐC3( néi tiÕp cïng ch¾n cung AB). ÐD1= ÐC3 => => ÐC2 = ÐC3 (hai gãc néi tiÕp ®êng trßn (O) ch¾n hai cung b»ng nhau) => CA lµ tia ph©n gi¸c cña gãc SCB. 3. XÐt DCMB Ta cã BA^CM; CD ^ BM; ME ^ BC nh vËy BA, EM, CD lµ ba ®êng cao cña tam gi¸c CMB nªn BA, EM, CD ®ång quy. 4. Theo trªn Ta cã => ÐD1= ÐD2 => DM lµ tia ph©n gi¸c cña gãc ADE.(1) 5. Ta cã ÐMEC = 900 (néi tiÕp ch¾n nöa ®êng trßn (O)) => ÐMEB = 900. Tø gi¸c AMEB cã ÐMAB = 900 ; ÐMEB = 900 => ÐMAB + ÐMEB = 1800 mµ ®©y lµ hai gãc ®èi nªn tø gi¸c AMEB néi tiÕp mét ®êng trßn => ÐA2 = ÐB2 . Tø gi¸c ABCD lµ tø gi¸c néi tiÕp => ÐA1= ÐB2( néi tiÕp cïng ch¾n cung CD) => ÐA1= ÐA2 => AM lµ tia ph©n gi¸c cña gãc DAE (2) Tõ (1) vµ (2) Ta cã M lµ t©m ®êng trßn néi tiÕp tam gi¸c ADE TH2 (H×nh b) C©u 2 : ÐABC = ÐCME (cïng phô ÐACB); ÐABC = ÐCDS (cïng bï ÐADC) => ÐCME = ÐCDS => => ÐSCM = ÐECM => CA lµ tia ph©n gi¸c cña gãc SCB. Bµi 16 Cho tam gi¸c ABC vu«ng ë A.vµ mét ®iÓm D n»m gi÷a A vµ B. §êng trßn ®êng kÝnh BD c¾t BC t¹i E. C¸c ®êng thẳng CD, AE lÇn lît c¾t ®êng trßn t¹i F, G. Chøng minh : Tam gi¸c ABC ®ång d¹ng víi tam gi¸c EBD. Tø gi¸c ADEC vµ AFBC néi tiÕp . AC // FG. C¸c ®êng th¼ng AC, DE, FB ®ång quy. Lêi gi¶i: 1. XÐt hai tam gi¸c ABC vµ EDB Ta cã ÐBAC = 900 ( v× tam gi¸c ABC vu«ng t¹i A); ÐDEB = 900 ( gãc néi tiÕp ch¾n nöa ®êng trßn ) => ÐDEB = ÐBAC = 900 ; l¹i cã ÐABC lµ gãc chung => DDEB ~ D CAB . 2. Theo trªn ÐDEB = 900 => ÐDEC = 900 (v× hai gãc kÒ bï); ÐBAC = 900 ( v× DABC vu«ng t¹i A) hay ÐDAC = 900 => ÐDEC + ÐDAC = 1800 mµ ®©y lµ hai gãc ®èi nªn ADEC lµ tø gi¸c néi tiÕp . * ÐBAC = 900 ( v× tam gi¸c ABC vu«ng t¹i A); ÐDFB = 900 ( gãc néi tiÕp ch¾n nöa ®êng trßn ) hay ÐBFC = 900 nh vËy F vµ A cïng nh×n BC díi mét gãc b»ng 900 nªn A vµ F cïng n»m trªn ®êng trßn ®êng kÝnh BC => AFBC lµ tø gi¸c néi tiÕp. 3. Theo trªn ADEC lµ tø gi¸c néi tiÕp => ÐE1 = ÐC1 l¹i cã ÐE1 = ÐF1 => ÐF1 = ÐC1 mµ ®©y lµ hai gãc so le trong nªn suy ra AC // FG. 4. (HD) DÔ thÊy CA, DE, BF lµ ba ®êng cao cña tam gi¸c DBC nªn CA, DE, BF ®ång quy t¹i S. Bµi 17. Cho tam gi¸c ®Òu ABC cã ®êng cao lµ AH. Trªn c¹nh BC lÊy ®iÓm M bÊt k× ( M kh«ng trïng B. C, H ) ; tõ M kÎ MP, MQ vu«ng gãc víi c¸c c¹nh AB. AC. Chøng minh APMQ lµ tø gi¸c néi tiÕp vµ h·y x¸c ®Þnh t©m O cña ®êng trßn ngo¹i tiÕp tø gi¸c ®ã. Chøng minh r»ng MP + MQ = AH. Chøng minh OH ^ PQ. Lêi gi¶i: 1. Ta cã MP ^ AB (gt) => ÐAPM = 900; MQ ^ AC (gt) => ÐAQM = 900 nh vËy P vµ Q cïng nh×n BC díi mét gãc b»ng 900 nªn P vµ Q cïng n»m trªn ®êng trßn ®êng kÝnh AM => APMQ lµ tø gi¸c néi tiÕp. * V× AM lµ ®êng kÝnh cña ®êng trßn ngo¹i tiÕp tø gi¸c APMQ t©m O cña ®êng trßn ngo¹i tiÕp tø gi¸c APMQ lµ trung ®iÓm cña AM. 2. Tam gi¸c ABC cã AH lµ ®êng cao => SABC = BC.AH. Tam gi¸c ABM cã MP lµ ®êng cao => SABM = AB.MP Tam gi¸c ACM cã MQ lµ ®êng cao => SACM = AC.MQ Ta cã SABM + SACM = SABC => AB.MP + AC.MQ = BC.AH => AB.MP + AC.MQ = BC.AH Mµ AB = BC = CA (v× tam gi¸c ABC ®Òu) => MP + MQ = AH. 3. Tam gi¸c ABC cã AH lµ ®êng cao nªn còng lµ ®êng ph©n gi¸c => ÐHAP = ÐHAQ => ( tÝnh chÊt gãc néi tiÕp ) => ÐHOP = ÐHOQ (t/c gãc ë t©m) => OH lµ tia ph©n gi¸c gãc POQ. Mµ tam gi¸c POQ c©n t¹i O ( v× OP vµ OQ cïng lµ b¸n kÝnh) nªn suy ra OH còng lµ ®êng cao => OH ^ PQ Bµi 18 Cho ®êng trßn (O) ®êng kÝnh AB. Trªn ®o¹n th¼ng OB lÊy ®iÓm H bÊt k× ( H kh«ng trïng O, B) ; trªn ®êng th¼ng vu«ng gãc víi OB t¹i H, lÊy mét ®iÓm M ë ngoµi ®êng trßn ; MA vµ MB thø tù c¾t ®êng trßn (O) t¹i C vµ D. Gäi I lµ giao ®iÓm cña AD vµ BC. Chøng minh MCID lµ tø gi¸c néi tiÕp . Chøng minh c¸c ®êng th¼ng AD, BC, MH ®ång quy t¹i I. Gäi K lµ t©m ®êng trßn ngo¹i tiÕp tø gi¸c MCID, Chøng minh KCOH lµ tø gi¸c néi tiÕp . Lêi gi¶i: 1. Ta cã : ÐACB = 900 ( néi tiÕp ch¾n nöc ®êng trßn ) => ÐMCI = 900 (v× lµ hai gãc kÒ bï). ÐADB = 900 ( néi tiÕp ch¾n nöc ®êng trßn ) => ÐMDI = 900 (v× lµ hai gãc kÒ bï). => ÐMCI + ÐMDI = 1800 mµ ®©y lµ hai gãc ®èi cña tø gi¸c MCID nªn MCID lµ tø gi¸c néi tiÕp. 2. Theo trªn Ta cã BC ^ MA; AD ^ MB nªn BC vµ AD lµ hai ®êng cao cña tam gi¸c MAB mµ BC vµ AD c¾t nhau t¹i I nªn I lµ trùc t©m cña tam gi¸c MAB. Theo gi¶ thiÕt th× MH ^ AB nªn MH còng lµ ®êng cao cña tam gi¸c MAB => AD, BC, MH ®ång quy t¹i I. 3. DOAC c©n t¹i O ( v× OA vµ OC lµ b¸n kÝnh) => ÐA1 = ÐC4 DKCM c©n t¹i K ( v× KC vµ KM lµ b¸n kÝnh) => ÐM1 = ÐC1 . Mµ ÐA1 + ÐM1 = 900 ( do tam gi¸c AHM vu«ng t¹i H) => ÐC1 + ÐC4 = 900 => ÐC3 + ÐC2 = 900 ( v× gãc ACM lµ gãc bÑt) hay ÐOCK = 900 . XÐt tø gi¸c KCOH Ta cã ÐOHK = 900; ÐOCK = 900 => ÐOHK + ÐOCK = 1800 mµ ÐOHK vµ ÐOCK lµ hai gãc ®èi nªn KCOH lµ tø gi¸c néi tiÕp. Bµi 19. Cho ®êng trßn (O) ®êng kÝnh AC. Trªn b¸n kÝnh OC lÊy ®iÓm B tuú ý (B kh¸c O, C ). Gäi M lµ trung ®iÓm cña ®o¹n AB. Qua M kÎ d©y cung DE vu«ng gãc víi AB. Nèi CD, KÎ BI vu«ng gãc víi CD. Chøng minh tø gi¸c BMDI néi tiÕp . Chøng minh tø gi¸c ADBE lµ h×nh thoi. Chøng minh BI // AD. Chøng minh I, B, E th¼ng hµng. Chøng minh MI lµ tiÕp tuyÕn cña (O’). Lêi gi¶i: 1. ÐBIC = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => ÐBID = 900 (v× lµ hai gãc kÒ bï); DE ^ AB t¹i M => ÐBMD = 900 => ÐBID + ÐBMD = 1800 mµ ®©y lµ hai gãc ®èi cña tø gi¸c MBID nªn MBID lµ tø gi¸c néi tiÕp. 2. Theo gi¶ thiÕt M lµ trung ®iÓm cña AB; DE ^ AB t¹i M nªn M còng lµ trung ®iÓm cña DE (quan hÖ ®êng kÝnh vµ d©y cung) => Tø gi¸c ADBE lµ h×nh thoi v× cã hai ®êng chÐo vu«ng gãc víi nhau t¹i trung ®iÓm cña mçi ®êng . 3. ÐADC = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => AD ^ DC; theo trªn BI ^ DC => BI // AD. (1) 4. Theo gi¶ thiÕt ADBE lµ h×nh thoi => EB // AD (2). Tõ (1) vµ (2) => I, B, E th¼ng hµng (v× qua B chØ cã mét ®êng th¼ng song song víi AD mµ th«i.) 5. I, B, E th¼ng hµng nªn tam gi¸c IDE vu«ng t¹i I => IM lµ trung tuyÕn ( v× M lµ trung ®iÓm cña DE) =>MI = ME => DMIE c©n t¹i M => ÐI1 = ÐE1 ; DO’IC c©n t¹i O’ ( v× O’C vµ O’I cïng lµ b¸n kÝnh ) => ÐI3 = ÐC1 mµ ÐC1 = ÐE1 ( Cïng phô víi gãc EDC ) => ÐI1 = ÐI3 => ÐI1 + ÐI2 = ÐI3 + ÐI2 . Mµ ÐI3 + ÐI2 = ÐBIC = 900 => ÐI1 + ÐI2 = 900 = ÐMIO’ hay MI ^ O’I t¹i I => MI lµ tiÕp tuyÕn cña (O’). Bµi 20. Cho ®êng trßn (O; R) vµ (O’; R’) cã R > R’ tiÕp xóc ngoµi nhau t¹i C. Gäi AC vµ BC lµ hai ®êng kÝnh ®i qua ®iÓm C cña (O) vµ (O’). DE lµ d©y cung cña (O) vu«ng gãc víi AB t¹i trung ®iÓm M cña AB. Gäi giao ®iÓm thø hai cña DC víi (O’) lµ F, BD c¾t (O’) t¹i G. Chøng minh r»ng: 1. Tø gi¸c MDGC néi tiÕp . 2. Bèn ®iÓm M, D, B, F cïng n»m trªn mét ®êng trßn 3. Tø gi¸c ADBE lµ h×nh thoi. 4. B, E, F th¼ng hµng 5. DF, EG, AB ®ång quy. 6. MF = 1/2 DE. 7. MF lµ tiÕp tuyÕn cña (O’). Lêi gi¶i: 1. ÐBGC = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => ÐCGD = 900 (v× lµ hai gãc kÒ bï) Theo gi¶ thiÕt DE ^ AB t¹i M => ÐCMD = 900 => ÐCGD + ÐCMD = 1800 mµ ®©y lµ hai gãc ®èi cña tø gi¸c MCGD nªn MCGD lµ tø gi¸c néi tiÕp 2. ÐBFC = 900 ( néi tiÕp ch¾n nöa ®êng trßn ) => ÐBFD = 900; ÐBMD = 900 (v× DE ^ AB t¹i M) nh vËy F vµ M cïng nh×n BD díi mét gãc b»ng 900 nªn F vµ M cïng n»m trªn ®êng trßn ®êng kÝnh BD => M, D, B, F cïng
File đính kèm:
 cac_dang_bai_tap_toan_hinh_hoc_thi_vao_lop_10_thpt.doc
cac_dang_bai_tap_toan_hinh_hoc_thi_vao_lop_10_thpt.doc

